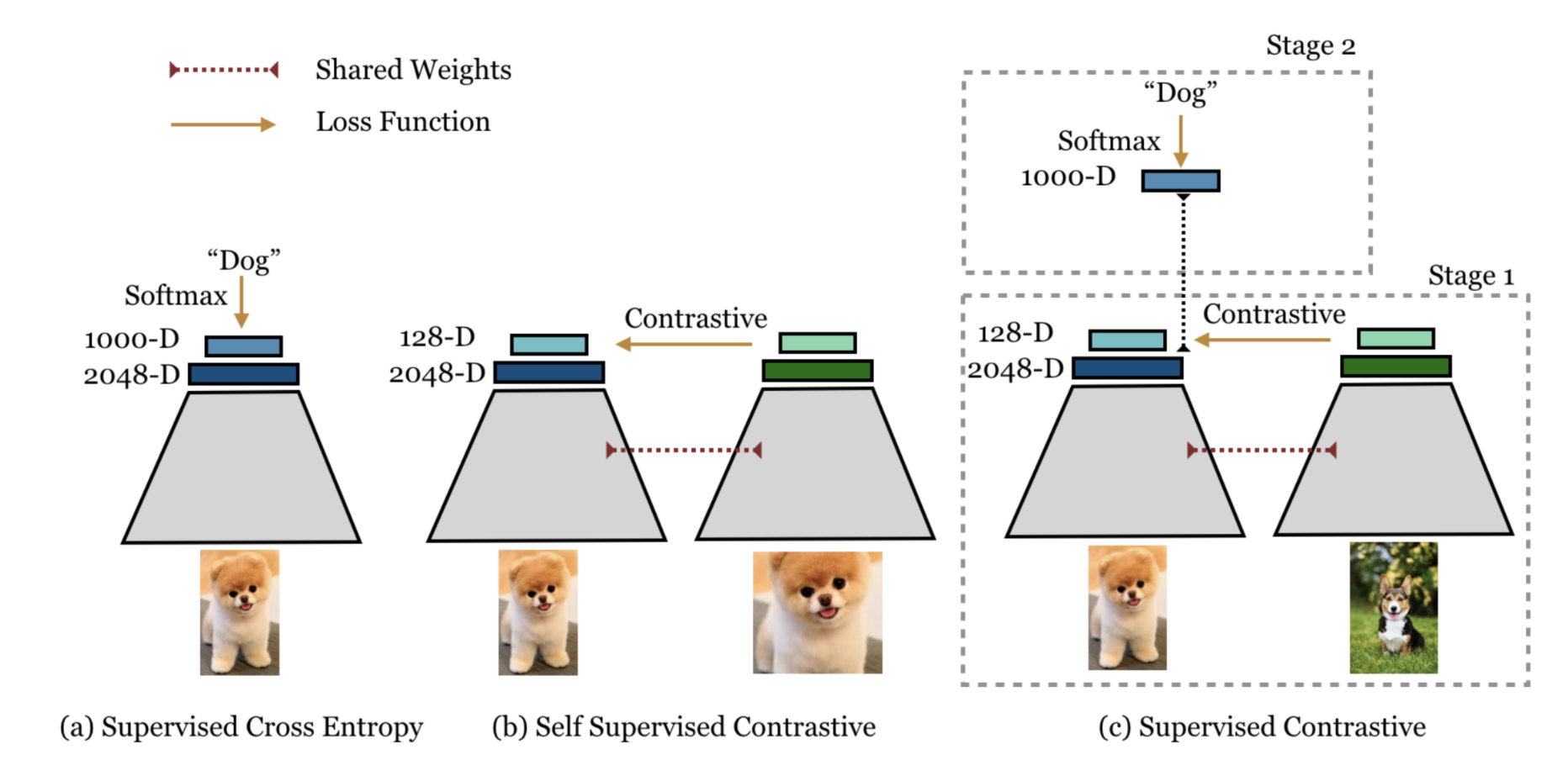
Supervised Contrastive Learning

论文来源：NeurIPS 2020

论文链接：https://arxiv.org/pdf/2004.11362.pdf

代码链接：https://github.com/HobbitLong/SupContrast

自监督对比学习（Self Supervised Contrastive Learning）

假设你有如下资源：

一个BackBone Network，用来提取图片feature，例如：ResNet-50, ResNet-101或者ResNet-200。
一个训练数据集，例如ImageNet

并且要求训练过程中不使用图片包含的Ground Truth类别信息（即不能用分类任务来训练），如何训练BackBone Network，使其能够为每张图片提取出好的feature？

这个问题的答案有很多，这里主要介绍一种“自监督对比学习”。对于自监督学习，核心是如何给数据自动产生一种标签，然后使用该标签来进行某种“监督学习”。例如：对于无标签的图片，可以把图片随机旋转一个角度 $\alpha$ （例如： $90^。,180^。，270^。$ ），然后用旋转后的图片作为输入，训练网络来预测图片到底旋转了哪个角度。作为本文涉及到的“自监督对比学习”，它的设定是这样的：

假设一个MiniBatch包含 $N$ 张图片，分别随机对每张图片进行两次Data Augmentation（裁剪、翻转等）处理，每张图片会得出两张新的图片，总共会得出 $2N$ 张新图片，作为后续网络输入进行训练。
经过BackBone Network计算后， $2N$ 张图片，会产生 $2N$ 个feature ，对每个feature进行normalization处理，使其变为单位向量。这样每个feature就落在了一个半径为1的超球面上(hypersphere)。得到的feature为： $\{z_1,z_2,…,z_i,…,z_j,…,z_{2N} \}$ 。
对于任意一张图片 $i$ ：

在其余的 $2N-1$ 张图片中，都存在一张图片 $j$ ，图片 $i$ 和 $j$ 来源于同一张图片（同一张图片随机Augmentation两次，得出的图片 $i$ 和 $j$ ）。因为它们来源于同一张图片，所以让图片 $i$ 和 $j$ 的feature越接近越好。
除了图片 $i$ 和 $j$ ，对于其余的 $2N-2$ 张图片，因为它们与图片 $i$ 来源于不同的图片，所以让它们的feature与图片 $i$ 的feature越远越好
可以看出，这种方法的本质是：分别用与图片 $i$ 来源相同的图片的feature、与图片 $i$ 来源不同的图片的feature，跟图片 [$i$ 的feature进行对比，然后让来源相同的图片feature越接近，来源不同的图片feature越远。按照这个要求，训练使用如下loss函数来训练模型：

$L^{self} = \sum\limits_{i \in I}L_i^{self} = - \sum\limits_{i\in I} \log \frac{exp(z_i\cdot z_{j(i)}/ \tau)}{\sum\limits_{a \in A(i)} \cdot exp(z_i \cdot z_k / \tau)}$

其中，$z_l = Proj(Enc(x_l))$为表征学习得到的特征， $\tau$ 是一个大于0的常数（论文中称为：a scalar temperature parameter），$\cdot$表示内积(inner product) $a \cdot b=|a||b| \cos \theta$，内积越大表示$\theta$越小，即两向量的夹角越小，即两向量更相似。

该Loss表示：

对于任意图片 $i$ ：

图片 $i$ 和 $j$ 的feature内积越小越好，$\cos\theta$越大，loss越小。
图片 $i$ 与来源不同的其它图片的feature内积的总和，越小越好。

这种方式虽然能学到不错的feature，但有一个不足是：没有考虑到属于同一个类的不同图片之间的feature的相关性。例如下图所示的情况：

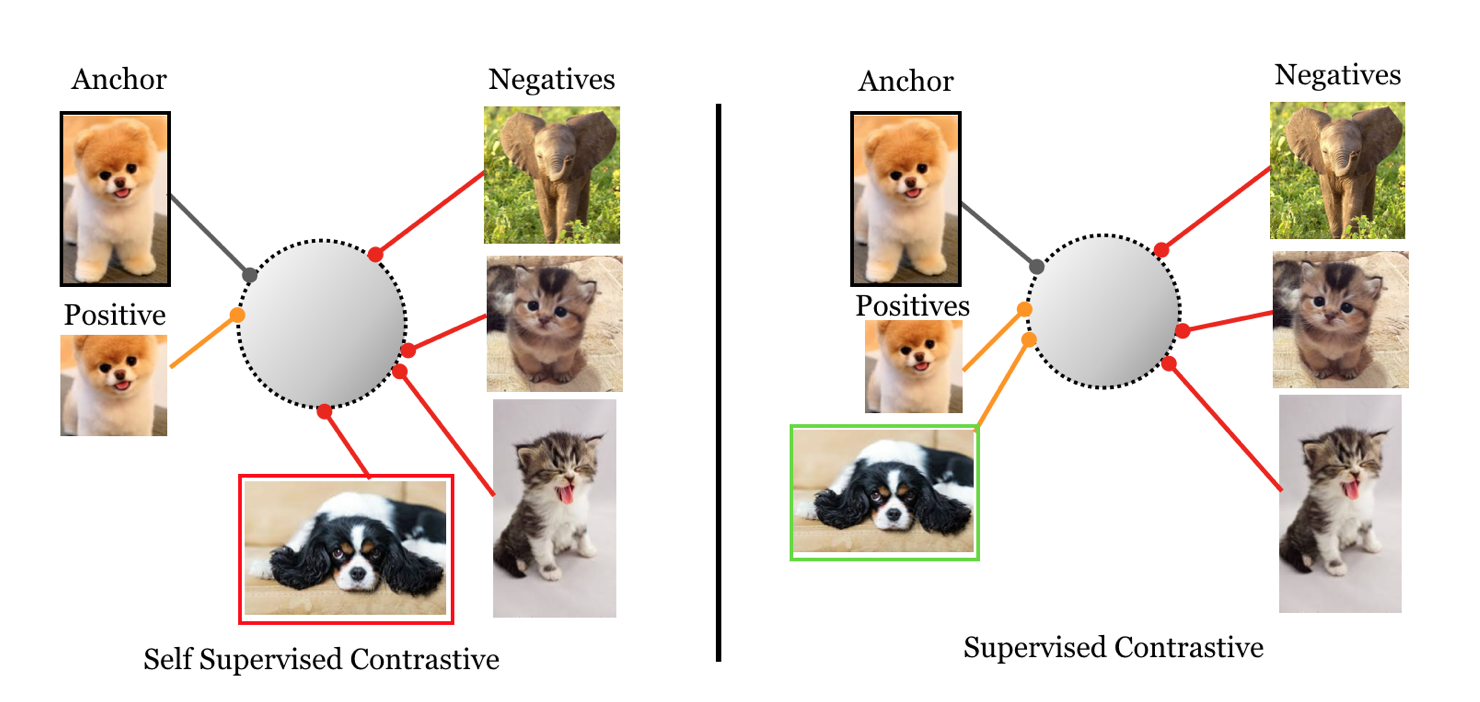
对于一张图片（左上角），来源相同的图片（左侧下方两张augmentation后的图片）的feature，在超球面上的距离很接近，来源不同的图片之间的feature的距离会比较远。但有一张与左上角图片属于同一类的图片（上图里面的红框图片），他的feature与左上角图片的feature的距离也会很远。

直觉上，同类图片的feature，应该也是越接近越好。但由于“自监督对比学习”的设定里面不使用图片所属的类别信息，所以无法知道哪些图片属于同一类，因此也无法让同类图片的feature彼此距离接近。

如果能使用图片的类别 label信息，是否能提高以上“自监督对比学习“的feature的质量？

监督对比学习（Supervised Contrastive Learning）

为了让同类图片的feature彼此接近，需要使用类别信息来判断哪些图片属于同一个类，因此，方法的名字从“自监督”变成了“监督”。对比学习的依据，从“是否来源于同一张图片“，变成了”是否属于同一个类“。训练使用的loss函数变为：

$\begin{array}{c} \mathcal{L}_{\text {out }}^{\text {sup }}=\sum\limits_{i \in I} \mathcal{L}_{\text {out }, i}^{\text {sup }}=\sum\limits_{i \in I} \frac{-1}{|P(i)|} \sum\limits_{p \in P(i)} \log \frac{\exp \left(\boldsymbol{z}_{i} \cdot \boldsymbol{z}_{p} / \tau\right)}{\sum_{a \in A(i)} \exp \left(\boldsymbol{z}_{i} \cdot \boldsymbol{z}_{a} / \tau\right)} \\ \mathcal{L}_{i n}^{s u p}=\sum\limits_{i \in I} \mathcal{L}_{i n, i}^{s u p}=\sum_{i \in I}-\log \left\{\frac{1}{|P(i)|} \sum\limits_{p \in P(i)} \frac{\exp \left(\boldsymbol{z}_{i} \cdot \boldsymbol{z}_{p} / \tau\right)}{\sum\limits_{a \in A(i)} \exp \left(\boldsymbol{z}_{i} \cdot \boldsymbol{z}_{a} / \tau\right)}\right\} \end{array}$

$P(i) \equiv \{ p \in A(i):\tilde{y_p} = \tilde{y_i}\}$，代表所有与下标为i的样本label相同的样本集合（正样本集合），$|P(i)|$为该集合的大小。

该loss表达的含义是：

对于任意图片 $i$

与图片 $i$ 属于同类的所有其它图片的feature，与图片 $i$ 的feature的内积的总和，越大越好
与图片 $i$ 不属于同类的所有其它图片的feature，与图片 $i$ 的feature的内积的总和，越小越好

前者的求和操作在$\log$外部，而后者在内部。作者在论文中论证了这两种损失函数的优劣，最终得出$L_{out}^{sup}$更好。

相比自监督对比损失，两种方式都有如下特性：

使用了大量正样本

自监督学习仅仅将data augmentation得到的样本作为正样本，而在有监督的设置中，通过data augmentation得到的正样本以及与anchor标签一样的正样本都对公式中的分子有贡献。

负样本越多，对比性越强

保留了对于负样本的求和，噪声样本越多，对比的效果越好。

具有发掘难正/负样本的内在能力

这两个损失函数的梯度鼓励从hard positive和hard negative中学习。