NLP中的语言模型(language model)

本文搬运自CSDN，并修改了其中一些错误。

什么是语言模型?

统计语言模型是一个单词序列上的概率分布，对于一个给定长度为m的序列，它可以为整个序列产生一个概率 P(w_1,w_2,…,w_m) 。其实就是想办法找到一个概率分布，它可以表示任意一个句子或序列出现的概率。

目前在自然语言处理相关应用非常广泛，如语音识别(speech recognition) , 机器翻译(machine translation), 词性标注(part-of-speech tagging), 句法分析(parsing)等。传统方法主要是基于统计学模型，最近几年基于神经网络的语言模型也越来越成熟。

Unigram models

Unigram models也即一元文法模型，它是一种上下文无关模型。该模型仅仅考虑当前词本身出现的概率，而不考虑当前词的上下文环境。概率形式为

$P ( w_1 , w_2 , . . . , w_m ) = P ( w_1 ) ∗ P ( w_2 ) ∗ . . . ∗ P ( w_m ) P(w_1,w_2,...,w_m)$

即一个句子出现的概率等于句子中每个单词概率乘积。
以一篇文档为例，每个单词的概率只取决于该单词本身在文档中的概率，而文档中所有词出现的概率和为1，每个词的概率可以用该词在文档中出现的频率来表示，如下表中

Terms	Probability
a	0.1
world	0.2
likes	0.05
we	0.03
share	0.26
…	…

对于这篇文档中，所有概率和相加为1，即

$\sum P(term) = 1$

n-gram模型

n-gram models也即n元语言模型，针对一个句子$w_1,w_2,…,w_m$的概率表示如下：

$P(w_1,w_2,...,w_m)= \prod_{i=1}^{m}P(w_i|w_1,...,w_{i-1})=\prod_{i=1}^{m}P(w_i|w_{i-(n-1),...,w_{i-1}})$

这里可以理解为当前词的概率与前面的n个词有关系，可以理解为上下文有关模型。

n-gram模型中的条件概率可以用词频来计算：

$P(w_i|w_{i-(n-1)},...,w_{i-1})=\frac{count(w_{i-(n-1)},...,w_{i-1},w_i)}{count(w_{i-(n-1)},...,w_{i-1})}$

这里举个栗子：我们的原始文档是 doc = “我不想写代码了” ，经过中文分词处理后为 words = [“我”, “不想”, “写”, “代码”, “了”]。

那么产生原始文档doc的概率为：
P(我, 不想, 写, 代码, 了) = P(我) x P(不想|我) x P(写|我, 不想) x P(代码|我, 不想, 写) x P (了|我, 不想, 写, 代码)

相乘的每个概率可以通过统计词频来获得：

n-gram	probability
P(不想 \| 我) =	count(我, 不想) / count(我)
P(写 \| 我, 不想) =	count(我, 不想, 写) / count(我, 不想)
P(代码 \| 我, 不想, 写) =	count(我, 不想, 写, 代码) / count(我, 不想, 写)
P(了 \| 我, 不想, 写, 代码) =	count(我, 不想, 写, 代码, 了) / count(我, 不想, 写, 代码)

如果像上面这样去计算，会疯掉的。。。这种计算太复杂了，所以我们是否可以简化只考虑少数的词呢，如二元bigram模型，当前词只与它前面的一个词相关，这样概率求解就简化很多：

$P(w_1,w_2,...,w_m)=\prod_{i=1}^{m}P(w_i|w_{i-(n-1),...,w_{i-1}}) = \prod_{i=1}^{m}P(w_i|w_{w_{i-1}})$

上面那个栗子也可以简化了：

P(我, 不想, 写, 代码, 了) = P(我) x P(不想|我) x P(写|不想) x P(代码|写) x P (了|代码)

相乘的每个概率就更简单了：

bigram	probability
P(不想｜我) =	count(我, 不想) / count(我)
P(写｜不想) =	count(不想, 写) / count(不想)
P(代码｜写) =	count(写, 代码) / count(写)
P(了｜代码) =	count(代码, 了) / count(代码)

这样我们只需要计算语料中每个词出现的次数，以及每两个词出现的次数，就可以求上面的概率了。

这里是以二元模型说明，你也可以使用三元(trigram)、四元模型，方法类似不在多说。前面提到的 Unigram模型其实就是一元模型。

神经网络语言模型(NNLM)

神经语言模型使用连续表示或词汇Embedding来进行预测。以神经网络为基础来训练模型。

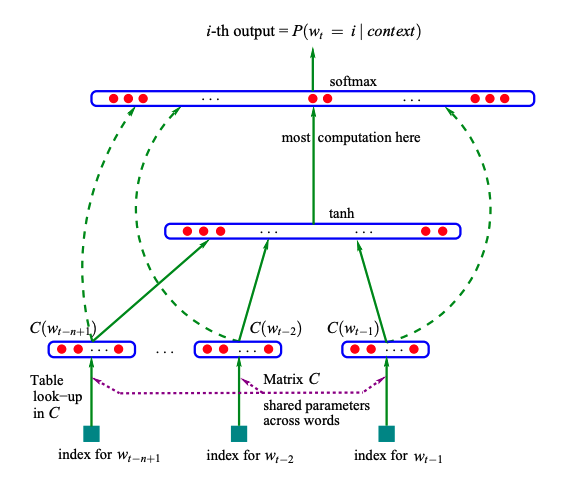
输入：n-1个之前的word（用词典库V中的index表示）

映射：通过|V|*D的矩阵C映射到D维

隐层：映射层连接大小为H的隐层

输出：输出层大小为|V|，表示|V|个词中每个词的概率

网络第一层：将 $C(w_{t-n+1}), … ,C(w_{t-2}),C(w_{t-1})$这n-1个向量首尾相接拼起来，形成一个(n-1)*m维的向量，记为输出x。

网络第二层：就是神经网络的隐藏层，直接使用 $d+Hx$ 计算得到，H是权重矩阵，d是一个偏置向量。然后使用tanh作为激活函数。

网络第三层：输出一共有|V|个节点，每个节点 $y_i$ 表示下一个词为i的未归一化log概率，最后使用softmax激活函数将输出值y归一化成概率。y的计算公式：

$y = b+Wx+Utanh(d+Hx)$

式中U是一个|V| X h 的矩阵，表示隐藏层到输出层的参数；W是|V| x (n-1)m的矩阵，这个矩阵包含了从输入层到输出层的直连边，就是从输入层直接到输出层的一个线性变换。

$p = softmax(y)$

word2vec模型

word2vec分为两个基础模型CBOW和Skip-gram，其中CBOW模型是根据上下文词预测当前词，Skip-gram模型是根据当前词预测它的上下文，其实都是在发现语料中局部词汇之间的共现关系。

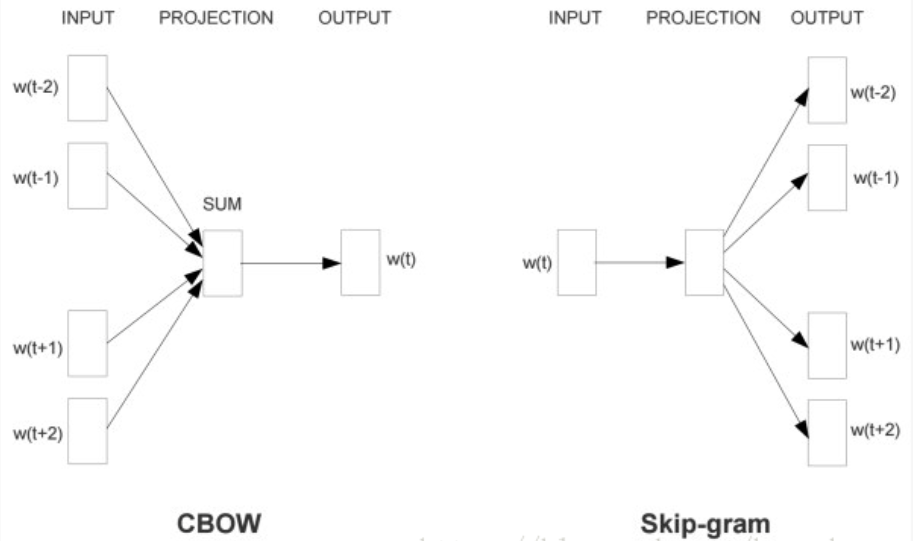
CBOW

CBOW模型是在语料中设置一个窗口，每次滑动这个窗口，根据窗口除中心词之前的其他词，来预测中心词，就是根据上下文窗口词预测当前中心词，还是以前面的例子具体说明一下，
原始doc = “我真不想写代码了”，分词后 words = [“我”, “真”, “不想”, “写”, “代码”, “了”]。
如果窗口window_size = 3, 则window1 = [“真”, “不想”, “写”]、window2 = [“不想”, “写”, “代码”]等3个词的窗口，对应CBOW模型的输入和输出：

input	output
[“真”, “写”]	“不想”
[“不想”, “代码”]	“写”

如果窗口window_size = 5, 则window1 = [“我”, “真”, “不想”, “写”, “代码”]、 window2 = [“真”, “不想”, “写”, “代码”, “了”] 等5个词的窗口，对应CBOW模型的输入和输出：

input	output
[“我”, “真”, “写”, “代码”]	“不想”
[“真”, “不想”, “代码”, “了”]	“写”

而具体计算是要获得每个输入词的向量表示，然后求和取平均值，最后完成词汇表大小的分类任务。
对应公式就是假设当前词是w，w对应的上下文窗口词是context(w)，windows_size = 2c + 1，context(w)由w前后各c个词构成。

输入层：包含context(w)中2c个词的词向量，$v(context(w)_1),v(context(w)_2)$，…。这里的词向量通过词编号映射得到，也就是我们模型要学习的词向量，词向量维度设为m。

投影层：对输入的2c个向量做求和累加，公式标识如下，其中 $x_w \in R^mx$

$x_w = \sum_{i=1}^{2c}v({Context(w)}_i)$

对应上面window_size = 5的第一个例子就是 $x_{不想}$ = v(我) + v(真) + v(写) + v(代码)。

输出层：对应输出层最直观的方法是，投影层得到的 $x_w$

直接乘以一个和词表大小一样的权重矩阵，然后过一层softmax函数得到词表大小的一个概率分布向量，取其中概率最大的为预测结果词。设U是一个$V × m$的矩阵，V对应词表大小，m对应词向量维度，b对应偏置项，我们可以得到上下文context(w)预测当前词w的概率分布。

$p(w|context(w)) = softmax(Ux_w + b)$

然后用概率分布$p(w|context(w))$与真实label的交叉熵作为损失函数，来训练模型。这里理论上可行，但是训练速度很慢，一般词表大小v都在几十万，每次求softmax是非常耗时。所以word2vec就在这个输出还用层次softmax来优化，从而加速模型训练过程。

Hierarchical Softmax（层次Softmax）

具体就是根据词表中词的出现频率作为权重来构造Huffman树，这样树的叶子节点对应的就是每个词，按照叶子节点对应的路劲就能找到每个词，简单理解就是我们用这样一颗树来存储我们的词表，可以加速输出层的计算。
具体过程首先定义几个变量：

$p^w$从根节点出发到词w对应叶子节点的路劲；
$l^w$ 路径 $p^w$ 中包含的结点个数；
$p_1^w,p_2^w,…,p_{l^w}^w$ 路径$p^w$中的$l^w$个节点，其中$p_1^w$表示根结点，$p_{l^w}^w$表示词$w$对应的结点；
$d_2^w,d_3^w,…,d_{l^w}^w \in \{0,1\}$ 词$w$的Huffman编码，它由$l^w-1$位编码构成，$d_j^w$表示路径$p^w$中第$j$个结点对应的编码（根结点不对应编码）
$\theta_1^w,\theta_2^w,…,\theta_{l^w-1}^w \in R^m$ 路径$p^w$中非叶子结点对应的向量，$\theta_j^w$表示路径$p^w$中第$j$个非叶子结点对应的向量。

这里为什么要给Haffuman树中的非叶子向量也定义一个同长的向量呢？其实它们只是辅助向量

计算概率的方法是对词w所在路径每个节点进行二分类，并把节点二分类的概率进行相乘，从而得到词w的概率$p(w|context(w))$。对应的二分类可以用逻辑回归，假设0代表正类，1代表负类，

正类概率：

$p(0|x_w^{T}) = \sigma (x_w^{T}) = \frac{1}{1 + e^{-x_w^{T}\theta}}$

负类概率：

$p(1|x_w^{T}) = 1 - \sigma (x_w^{T})$

求得词w对应路劲上每个节点的分类概率后，$p(w|context(w))$对应跟一般的概率表示：

$p(w|context(w)) = \prod_{j=2}^{l^w} p(d_j^w|x_w,{\theta}_{j-1}^w)$

其中根据逻辑回归可得：

$p(d_j^w|x_w,{\theta}_{j-1}^w) = \begin{cases} σ(x_w^T θ_{j−1}^w)&,&d_j^w=0 \\\\ 1−σ(x_w^Tθ_{j−1}^w)&,&d_j^w=1 \end{cases}$

上式也可以表示为：

$p(d_{j}^{w}|x_{w},{\theta}_{j-1}^{w}) = {[\sigma(x_{w}^{T}{\theta}_{j-1}^{w})]^{1-d_{j}^{w}}}\cdot [1- \sigma(x_{w}^{T}{\theta}_{j-1}^{w})]^{d_{j}^{w}}$

p(w|context(w))可以表示为：

$p(w|context(w)) = \prod_{j=2}^{l^w}p(d_j^w|x_w,{\theta}_{j-1}^w) = \prod_{j=2}^{l^w}[\sigma(x_w^T{\theta}_{j-1}^w)]^{1-d_j^w}\cdot [1- \sigma(x_w^T{\theta}_{j-1}^w)]^{d_j^w}$

优化的目标，对数似然函数为：

$L = \sum_{w\in C}\log{p(w|Context(w))}$

将p(w|context(w))带入到对数似然函数中，得到最终的优化函数：

$L = \sum_{w\in C}\log{\prod_{j=2}^{l^w}[\sigma(x_w^T{\theta}_{j-1}^w)]^{1-d_j^w}\cdot [1- \sigma(x_w^T{\theta}_{j-1}^w)]^{d_j^w}} \\ =\sum_{w\in C}\sum_{j=2}^{l^w}\{(1-d_j^w)\log[\sigma(x_w^T{\theta}_{j-1}^w)]+d_j^w\log[1- \sigma(x_w^T{\theta}_{j-1}^w)]\}$

Skip-gram

Skip-gram模型也要设置一个窗口，每次滑动窗口，根据窗口中心词预测窗口内其他词，就是根据当前词预测上下文窗口词。还是以例子先理解一下。
原始doc = “我不想写代码了”，分词后 words = [“我”, “真”, “不想”, “写”, “代码”, “了”]。
如果窗口window_size = 3，则window1 = [“真”, “不想”, “写”]、window2 = [“不想”, “写”, “代码”]，对应Skip-gram模型的输入和输出：

input	context
“不想”	[“真” ,“写” ]
“写”	[“不想” ,“代码”]

如果窗口window_size = 5，则window1 = [“我”, “真”, “不想”, “写”, “代码”]、window2 = [“真”, “不想”, “写”, “代码”, “了”]，对应Skip-gram模型的输入和输出：

input	context
“不想”	[“我” ,“真” ,“写”,“代码” ]
“写”	[“真”,“不想”, “代码”, “了” ]

Skip-gram中给出当前词w，需要预测它的上下文词Context(w)，概率表示如下：

$p(Context(w)|w) = \prod_{u\in Context(w)}p(u|w)$

Hierarchical Softmax（层次Softmax）

类似前面CBOW模型，输出层也是用层次softmax来优化。上面p(u|w)就可以表示成词w的向量表示 $x_w$ 与词u的哈夫曼树路径表示相乘。

$p(u|w) = \prod_{j=2}^{l^u}p(d_j^u|x_w,\theta _{j-1}^u)$

路径中每一步概率可表示为：

$p(d_j^u|x_w,{\theta}_{j-1}^u) = {[\sigma(x_w^T{\theta}_{j-1}^u)]^{1-d_j^u}}\cdot [1- \sigma(x_w^T{\theta}_{j-1}^u)]^{d_j^u}$

同样对优化的目标，对数似然函数为：

$L = \sum_{w\in C}\log{p(Context(w)|w)}$

带入p(u|w) 得到最终的优化函数：

$L = \sum_{w\in C}\log\prod_{u\in Context(w)}p(u|w) = \sum_{w\in C}\sum_{u\in Context(w)}\log p(u|w) \\ = \sum_{w\in C}\sum_{u\in Context(w)}\log{\prod_{j=2}^{l^u}[\sigma(x_w^T{\theta}_{j-1}^u)]^{1-d_j^u}\cdot [1- \sigma(x_w^T{\theta}_{j-1}^u)]^{d_j^u}} \\ =\sum_{w\in C}\sum_{u\in Context(w)}\sum_{j=2}^{l^u}\{(1-d_j^u)\log[\sigma(x_w^T{\theta}_{j-1}^u)]+d_j^u\log[1- \sigma(x_w^T{\theta}_{j-1}^u)]\}$

关于word2vec中的数学原理，这篇博客讲的很详细word2vec 中的数学原理详解

NLP中的语言模型(language model)

本文搬运自CSDN，并修改了其中一些错误。

什么是语言模型?

Unigram models

n-gram模型

神经网络语言模型(NNLM)

word2vec模型

CBOW

Hierarchical Softmax（层次Softmax）

正类概率 ：

负类概率：

Skip-gram

Hierarchical Softmax（层次Softmax）

正类概率：