Joint Embedding of Words and Labels for Text Classification

发表于 | 分类于 |
字数统计: 1.1k | 阅读时长 ≈ 4

Joint Embedding of Words and Labels for Text Classification

论文来源：ACL 2018
论文链接：https://arxiv.org/abs/1805.04174
代码链接：https://github.com/guoyinwang/LEAM

作者提出使用word和label的一个联合embedding来更好的学习文本表示。

目前大多数的文本分类方法都是基于CNN和RNN，并且还会加入attention机制来获取文本中的word的依赖和重要度从而更好的学习文本的representation。作者在本文中也沿着这条主线进行探索，但是与之前的方法不同的是作者引入了文本的label信息来更好的学习文本表示，这也是本文的最大贡献与创新，即提出了一个Label-Embedding Attentive Model(LEAM)。该模型学习word和label在同一空间内的embedding，利用text和label的相关性构建文本表示。

符号表示

$⊘$表示element-wise的除法。

训练集为$S=\{(X_n,y_n)\}_{n=1}^N$

$X_i$为文本序列，$y_i$为其对应标记。

针对单标记任务， $y_i$ 是一个one-hot vector，而针对多标记任务， $y_i$ 是一个二值向量。举个例子，假设有5个类别，分别是1，2，3，4，5。如果某个样本对应类别3，在单标记中 $y_i$ 为(0,0,1,0,0)。如果某个样本同时属于类别2和4，则 $y_i$ 为(0,1,0,1,0)。模型的目标是学习一个从 $X$ 到 $y$ 的映射，使得下式最小

其中 $\delta$ 是损失函数。 $X_i$ 中的每个word都是一个one-hot vector $△^D$ ,D是字典的大小。而word embedding就是做一个 $△^D$ 到 $R^P$ 的映射，P是embedding的维度，用 $v_i$ 表示第 $i$ 个word的embedding。

模型详解

作者将文本分类看作三个函数的组合， $f=f_0∘f_1∘f_2$,

  • $f_0$ 是word embedding的函数，
  • $f_1$ 是将word embedding进行聚合得到文本表示的函数，
  • $f_2$ 是利用文本表示进行分类的函数。
    设计 $f_1$ 的方法分为两大类，其中一类是将该过程看作一个黑盒，利用各种深度模型学习映射，而另一个是利用简单的max pooling或者mean pooling。但无论怎样，这两类都只利用了文本word的信息。可以看出，只有 $f_2$ 利用了类别信息，而类别的影响对于 $f_0$ 和 $f_1$ 都是间接的。因此，作者提出在每个过程中都使用标记信息，模型如下

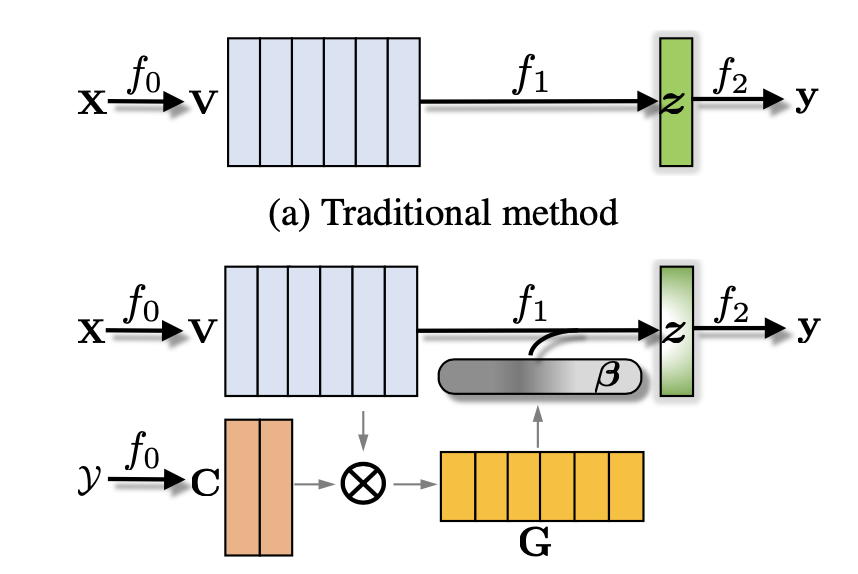
$f_0$: 学习label的embedding作为“anchor points”来影响word embedding，

$f_1$: 利用label和word之间的相关性进行word embedding的聚合。

$f_2$: 对于单标签问题和多标签问题有不同的处理方法，具体的看后面讲解。

首先将单词和标签嵌入到一个联合空间中：

$△^D \rightarrow R^P$ , $𝚢 \rightarrow R^P$

作者使用cosine相似度来计算每对label-word之间的相似度：

$G=(C^TV)⊘\hat{G}$

$C$是label embedding的矩阵，$C=[c_i,…,c_K]$,$K$为类的数量

$\hat{G}$是大小为$K×L$的归一化矩阵。$\hat{G}$中的每个元素为$\hat{g}_{kl}=||c_k|| \; ||v_l||$

为了把握连续单词之间的空间信息并引入非线性，作者对$G$进行了概括处理。

选取以$l$为中心,长度为$2r+1$的矩阵块$G_{l-r:l+r}$

$u_l = ReLU(G_{l−r:l+r}W_1 + b_1)$

$W_1∈R^{2e+1} \qquad b_1∈R^K \qquad u_l∈R^K$

$m_l=max_pooling(u_l)$

$\beta=SoftMax(m)$

$\beta_l = \frac{\exp \left(m_{l}\right)}{\sum_{l^{\prime}=1}^{L} \exp \left(m_{l^{\prime}}\right)}$

$z=\sum \limits_{l} \beta_lv_l$

损失函数

单标记问题，训练目标为:

$\underset{f \in F}{\min} \frac{1}{N} \sum\limits_{n=1}^{N} C E\left(y_{n}, f_{2}\left(z_{n}\right)\right)$

$CE(x,y)$表示两个概率向量$x,y$的交叉熵

这时,$f_2(z_n)=SoftMax(z_n’)$

$z_n’=W_2z_n+b_2,W_2∈R^{K×P},b_2∈R^K$

多标记问题，可以将其拆解为K个单标记问题，目标函数为下式

$\underset{f \in F}{\min} \frac{1}{N K} \sum\limits_{n=1}^{N} \sum\limits_{k=1}^{K} C E\left(y_{n k}, f_{2}\left(z_{n k}\right)\right)$

这时，$f_2(z_{nk})=\frac{1}{1+exp(z_{nk}’)}$,$z_{nk}’$是$z_n’$的第$k$列。

同时，作者希望label embedding能起到“anchor point”的作用，也就是相同类别的文本表示之间的距离小于不同类别的文本表示之间的距离。因此作者加入了一个正则化项

$\underset{f \in F}{\min} \frac{1}{K} \sum\limits_{n=1}^{K} C E\left(y_{k}, f_{2}\left(c_{k}\right)\right)$

0%