GILE A Generalized Input-Label Embedding for Text Classification

发表于 | 分类于 |
字数统计: 1.8k | 阅读时长 ≈ 7

GILE: A Generalized Input-Label Embedding for Text Classification

论文来源：TACL 2019
论文链接：https://arxiv.org/abs/1806.06219
代码链接：https://github.com/idiap/gile

启发：

现有的很多研究都是使用标签集合的k-hot向量进行训练。标签都只是被当成一个没有任何语义和标签空间结构的符号，而没有使用潜在的语义知识来描述输出的标签。
单词的语义描述已经被证实属于表示输入很有帮助，那么我们可以推断，对标签的语义描述应该也具有相同的效果。

做了什么：

  • 作者鉴定了现有的联合输入标签模型的关键理论和实践限制。
  • 作者在先前联合标签输入模型的基础上提出了一种新颖的带有灵活参数化的联合输入标签嵌入，并解决了现有模型的一些问题。
  • 作者提供经验证据表明，作者的模型优于忽略标签语义的单语言和多语言模型，并且在可见标签和不可见标签上的标签都要优于之前的联合输入标签模型。

    动机：

    先前的工作通过联合输入标签空间利用了标签文本中的知识，起初用于图像分类中。 这样的模型在训练过程中同时概况可见和不可见的标签，并且在大量标签集上的扩展很好。 不过它还是具有下面三种限制：
  • 因为它的双向线性关系，所以它们的嵌入无法捕获复杂的标签关系。
  • 因为输出层依赖于文本和标签的编码的维度所以输出层的参数比较死板。
  • 在可见标签上使用交叉熵损失函数的分类器表现的更好。

文本分类的背景知识:

$D = \{(x_i,y_i),i=1,…,N\}$

$x_i$表示第i个文本，$x_i=\{w_{11},w_{12},…,w_{K_i,T_{K_i}}\}$

$K_i$表示是第i个文本中的句子数量,$T_{K_i}$表示该句子的单词数量。

$y_i=\{y_{ij}∈\{0,1\},j=1,…,k\}$ $k$表示标签的数量。

$c_i=\{c_{j1},c_{j2},…,c_{j,L_j}|j=1,…,k\}$ 表示标签$j$的描述。$L_j$表示描述的单词数量。

在训练过程中只给文本和他们的可见标签D。我们的目标是训练一个分类器在可见标签$Y_s$的样本集合和不可见标签$Y_u$的样本集合上都能预测。 $Y_s∩Y_u=Ø,Y_s∪Y_u=Y$

输入的文本表示：

作者使用多层注意力网络 (HANs,hierarchical attention networks)来给输入文本编码。HANs在单语言和多语言分类上都有不错的竞争力。

输入：文本$x$ —> 输出：文本向量$h$ 。 输入的文本单词和标签单词都是用$d$维的向量$E$来表示。

$E∈IR^{|V|×d}$ 。$V$是词汇表， $d$是词嵌入的维度。

编码：

$g_w$对句子$i$,$\{w_{it}|t=1,2…,T_i\}$ 进行编码。
$h_{w}^{(it)}=g_w(w_{it}),t∈[1,T_i]$

将单词矩阵$\{h_{w}^{(it)}|t=1,…,T_i\}$联合(combining)成一个句子向量$s_i∈IR^{d_w}$,$d_w$是单词编码的维度。

$g_s$对句子序列$h_s^{(i)}=\{s_i|i=1,…,K\}$进行编码。

$g_w,g_s$可以是任何前向反馈网络，比如RNN或者GRU。

注意力：

$α_w,α_s$是注意力参数，用于衡量隐藏状态向量的重要程度。

$s_i=\sum\limits_{t=1}^{T_i} α_w^{(it)} h_w^{(it)}$

$=$

$\sum\limits_{t=1}^{T_i} \frac{exp(v_{it}^Tu_w)}{\sum_jexp(v_{ij}^Tu_w)} h_{w}^{it}$

$v_{it}=f_w(h_w^{(it)})$是$W_w$作为参数的全连接网络

HANs网络结构：

hans

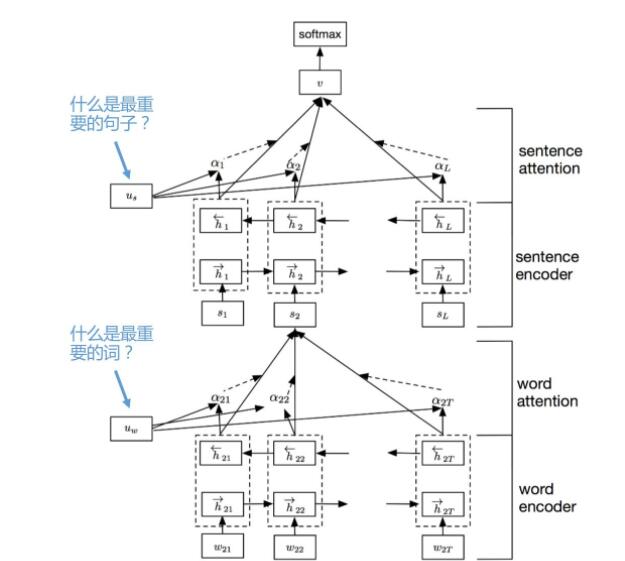
标签表示：

标签编码使用标签描述$c_j$作为输入，并输出一个标签向量$e_j∈IR^{d_c} ∀j=1,…,k.$考虑到效率方面作者使用简单的无参数的方式来计算$e_j$。直接使用描述中单词向量的平均值来描述标签$j$，$e_j=\frac{1}{L_j}\sum\limits_{t=1}^{L_j}c_{jt}$。将所有标签向量连接成一个矩阵，得到标签嵌入$ε∈IR^{|y|×d}$。

输出层参数化：

传统的线性单元：

最传统的输出层包含一个具有$W∈IR^{d_h×|y|}$和$b∈IR^{|y|}$的线性单元，并使用softmax或者sigmoid等激活函数进行激活。$d_h$是编码器的隐藏层表示$h$的维度。

$p(y|x)=∝exp(W^Th+b)$

$W$可以单独训练或者令$W=E^T$

无论是那种方式，模型的参数通常都是通过交叉熵损失函数来学习的。然而在两种情况下他们都无法适用于在训练过程中没有看见的标签。因为每个标签都学习了适用于特定那个标签的参数，所以未出现的标签的参数无法被学习到。

所以作者尝试使用可以处理不可见标签的模型。

双向输入标签单元：

因为标签编码器的参数是共享的，所以联合输入输出嵌入模型可以归纳可见标签和不可见标签。

  • 双线性排序函数：
    $f(x,y)=εωh$

    $ε∈IR^{|y|×d}$ 表示标签嵌入。
    $ω∈IR^{d×d_h}$是双向嵌入。

    这个函数允许使用铰链损失函数对标签y根据和x的相关性进行排序，不过这样就失去了条件概率。

    限制：

  • $f(x,y)=εωh$只能通过$ω$来捕获文本编码$h$和标签嵌入$ε$之间的线性关系。但是不同标签之间的关系是非线性的。 所以一个更合理的形式是引入非线性函数$σ(·)$

    输入结构：$σ(εω)h$
    输出结构：$σε(ωh)$

  • 因为参数$ω$的大小被$ε$和$h$的大小限制了，所以输出层的能力不好控制。

  • 它的损失函数是优化一个排名而不是分类表现。

提出的用于文本分类的输出层参数化

作者为神经文本分类提出了一种新的输出层参数化，包含了归纳输入标签嵌入从而获取标签结构，文本编码的结构和它们两种之间的关系。然后使用一个和标签集合大小无关的分类单元。

net

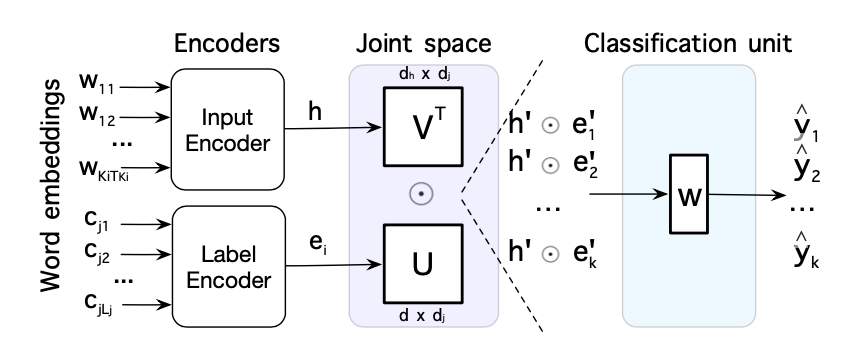
$e^j$是标签嵌入矩阵$ε$的第$j$行。

$e_j’=g_{out}(e_j)=σ(e_jU+b_u)$

$h’=g_{in}(h)=σ(Vh+b_v)$

传统的概率输出如下所示：

$p(y|x)∝exp(ε’h’)\\ \qquad \quad∝exp(g_{out}(ε)g_{in}(h)) \\ \qquad \quad∝exp(σ(εU+b_u) σ(Vh+b_v))$

作者提出了只依赖于联合输入标签空间的分类器

联合空间表示为：

$g_{joint}^{(ij)}=g_{in}(h_i)⊙g_{out}(e_j)$

$p_{val}^{ij}=g_{joint}^{(ij)}w+b$

$P_{v a l}^{(i)}=\left[\begin{array}{c}p_{v a l}^{(i 1)} \\ p_{v a l}^{(i 2)} \\ \cdots \\ p_{v a l}^{(i k)}\end{array}\right]=\left[\begin{array}{c}g_{j o i n t}^{(i 1)} w+b \\ g_{j o i n t}^{(i 2)} w+b \\ \cdots \\ g_{j o i n t}^{(i k)} w+b\end{array}\right]$

$\hat{y_i} = \hat{p} (y_{i} | x_{i})=\frac{1} {1+e^{-P_{val}^{(i) } } }$

0%